728x90
17611번: 직각다각형
입력의 첫 줄에는 단순직각다각형의 꼭지점의 개수를 나타내는 정수 n(4 ≤ n ≤ 100,000)이 주어지고, 이어지는 n개 줄 각각에 단순직각다각형 꼭지점의 좌표 (xi, yi)가 차례대로 주어진다. 주어지
www.acmicpc.net

1. 문제 요약
다각형의 좌표가 주어지고 수직선과, 수평선에 대하여 해당 다각형의 수직선분과, 수평선분이 가장 많이 교차하는 횟수를 구하라.
2. 접근 방법
백준 - 3020 개똥벌레 [누적합][이모스]
3020번: 개똥벌레 개똥벌레 한 마리가 장애물(석순과 종유석)로 가득찬 동굴에 들어갔다. 동굴의 길이는 N미터이고, 높이는 H미터이다. (N은 짝수) 첫 번째 장애물은 항상 석순이고, 그 다음에는 종
e-room.tistory.com
해당 문제 다각형의 좌표가 주어집니다만, 다각형으로 생각하지 않으면(?)
이모스 알고리즘을 사용하면 쉽게 풀이할 수 있습니다. (위 링크 참조)
12
0 0
0 3
1 3
1 1
2 1
2 3
5 3
5 0
4 0
4 2
3 2
3 0
위 다각형은 위 좌표를 다각형으로 표현한 것입니다.
해당 다각형을 수직과, 수평 선분으로 분리를 하면, 다음과 같은 형태를 얻을 수 있습니다.
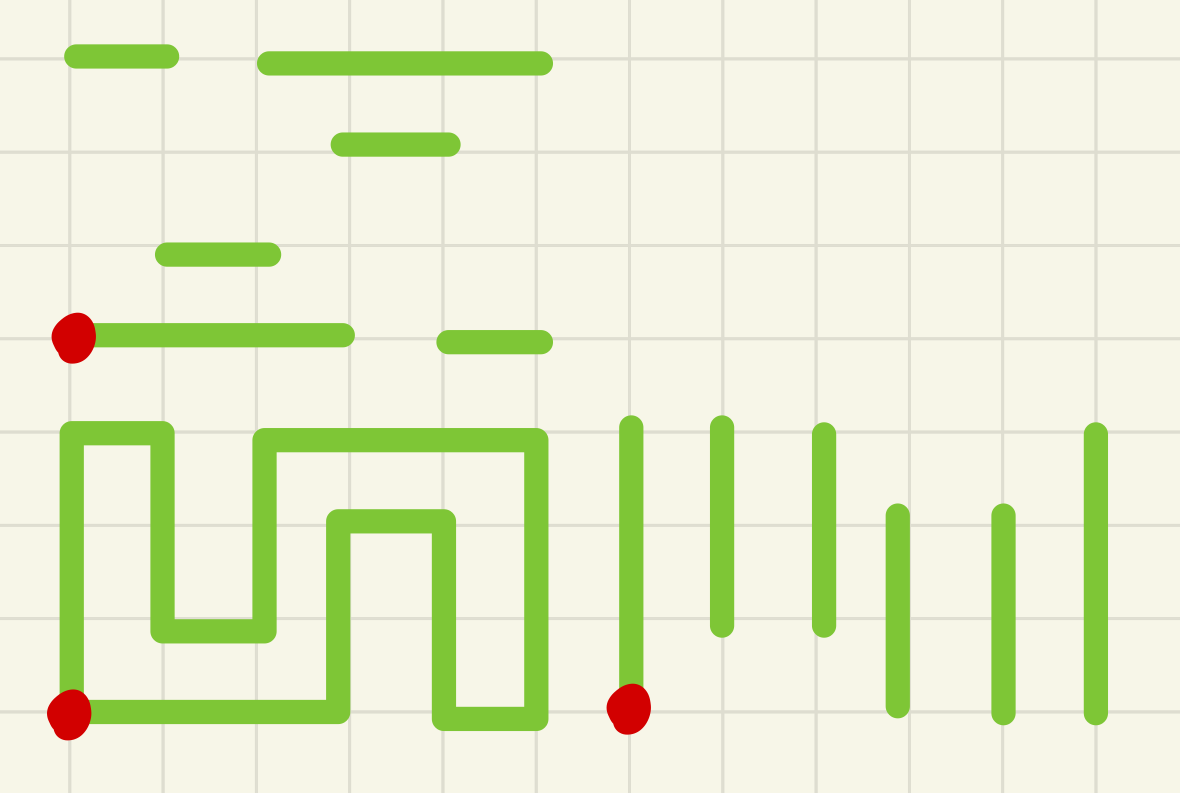
이런 식으로 주어진 좌표를 다각형으로 생각하지 않고, 두 가지 케이스의 이모스 장애물이 주어졌다고 생각하시면 굉장히 쉽습니다.
이모스 알고리즘 두 번 적용해서 두 가지 케이스 중 큰 값을 출력하면 됩니다.
3. 파이썬
def solution(arr: list, n: int):
# 보정
temp = min(arr)
if temp != 0:
for i in range(n):
arr[i] -= temp
# 계산
result = [0] * (max(arr)+1)
for i in range(n-1, -1, -1):
result[min(arr[i], arr[i-1])] += 1
result[max(arr[i], arr[i-1])] -= 1
# 누적합 계산
for i in range(1, len(result)-1):
result[i] += result[i-1]
return max(result[:-1])
4. 자바
static int solution(int[] arr, int n) {
// 보정
int temp = min(arr);
if (temp != 0) {
for (int i = 0; i < n; i++) {
arr[i] -= temp;
}
}
// 계산
int[] result = new int[max(arr) + 1];
for (int i = 0; i < n - 1; i++) {
result[Math.min(arr[i], arr[i + 1])] += 1;
result[Math.max(arr[i], arr[i + 1])] -= 1;
}
// 계산 - 맨처음 요소와 맨마지막 요소 추가 계산
result[Math.min(arr[0], arr[n - 1])] += 1;
result[Math.max(arr[0], arr[n - 1])] -= 1;
// 누적합 계산
for (int i = 1; i < result.length - 1; i++) {
result[i] += result[i - 1];
}
return max(result);
}
5. 전체 코드
728x90
'개발일지 > Algorithm' 카테고리의 다른 글
| 백준 - 15650 N과 M (2) [조합] (0) | 2023.09.27 |
|---|---|
| 백준 - 15649 N과 M (1) [순열] (0) | 2023.09.26 |
| 백준 - 3020 개똥벌레 [누적합][이모스] (0) | 2023.09.24 |
| 백준 - 11660 구간 합 구하기 5 [DP] (0) | 2023.09.23 |
| 백준 - 14719 빗물 [구현] (0) | 2023.09.22 |
