시간 복잡도
필요로 하는 시간을 따지는 것 : 입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 얼마나 걸리는가?
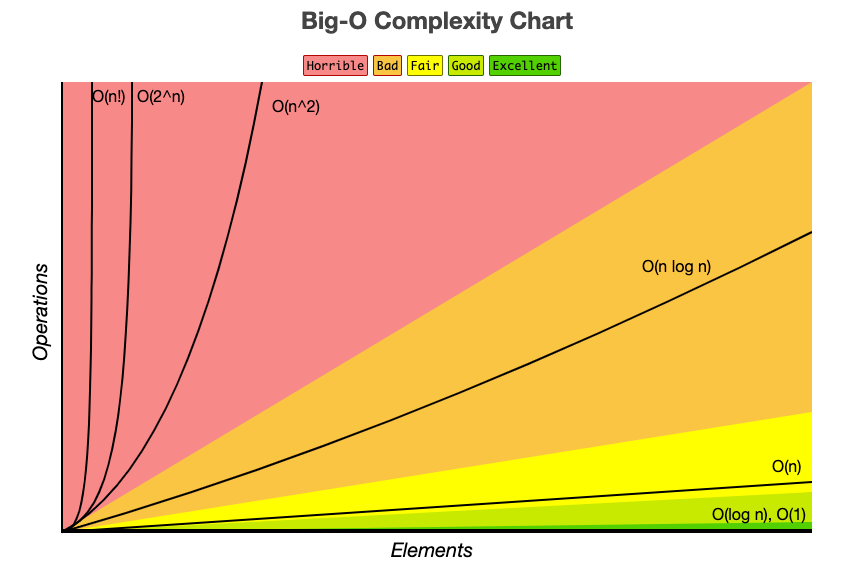
BIig-O 표기법
시간 복잡도를 표기하는 방법은 3가지가 있다
- Big-O (빅-오) - 최악 : "최대 이 정도까지 시간이 걸린다"
- Big-Ω (빅-오메가) - 최선 : "최소한 특정 시간 이상이 걸린다"
- Big-θ (빅-세타) - 평균 : "보통 이 정도 시간이 걸린다"
이 중 Big-O 표기법이 가장 자주 사용된다
다른 방법처럼 최악의 경우가 일어나지 않기를 바라는 것보다는 최악의 경우도 고려하여 대비하는 것이 바람직하다
O(1)
입력값의 크기와 관계없이 같은 시간이 걸린다
constant complexity라고 하며, 입력값이 증가하더라도 시간이 늘어나지 않는다
public static int O_1(int[] arr, int index) {
return arr[index];
}
int[] arr = new int[]{1, 2, 3, 4, 5};
int index = 1;
int results = O_1(arr, index);
System.out.println(results); // 2O(n)
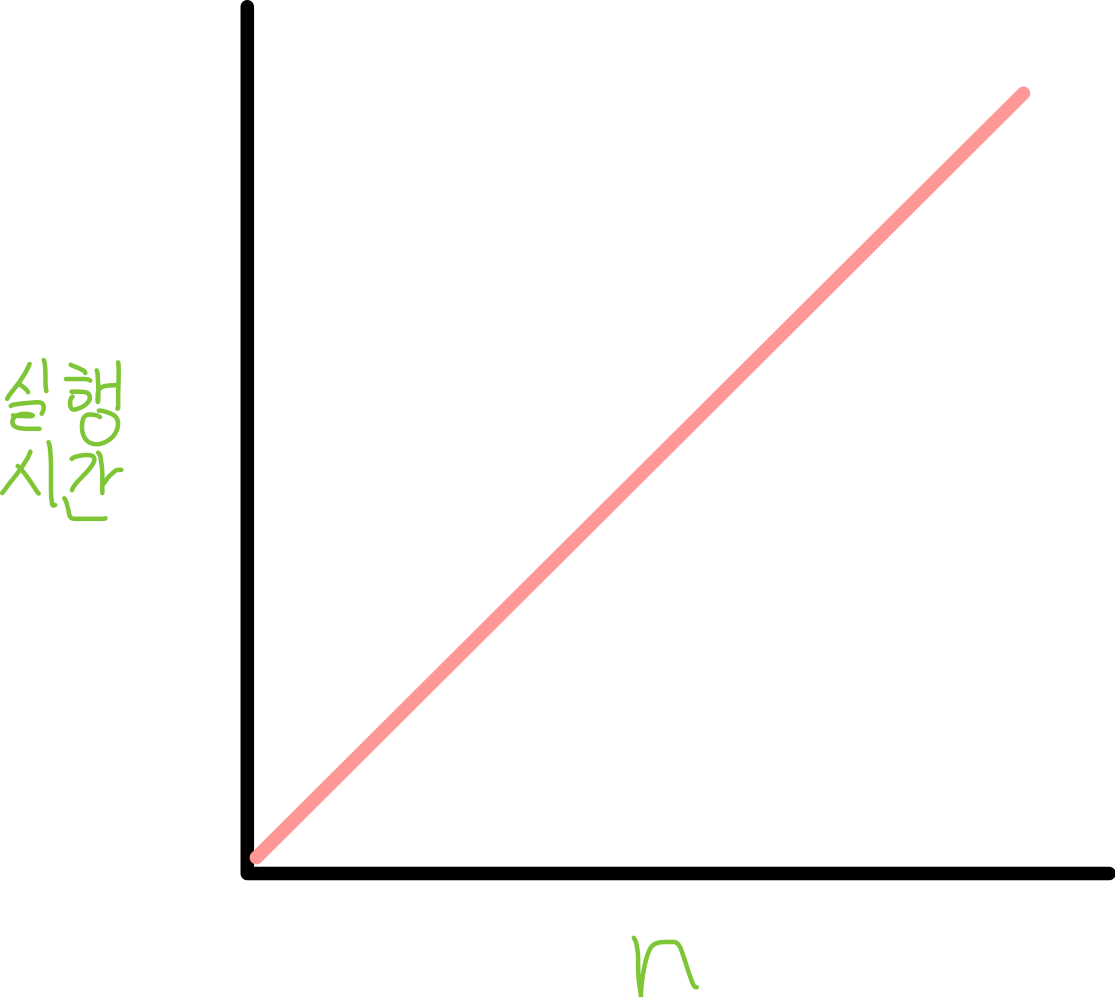
선형 복잡도(linear complexity)라고 부르며, 입력값이 증가함에 따라 시간 또한 같은 비율로 증가한다
public void O_n(int n) {
for (int i = 0; i < n; i++) {
System.out.println("안녕");
}
}
public void O_n2(int n) {
for (int i = 0; i < n * 2; i++) {
System.out.println("안녕2");
}
}❗️ O_n2 알고리즘은 입력값이 1 증가할 때마다 실행시간이 2씩 증가한다
이걸 보고 "그렇다면 이 알고리즘은 O(2n)이라고 표현하는 건가?" 라고 생각할 수 있는데
Big-O 표기법에서는 n앞의 수와 관계없이 모두 O(n)으로 표기한다
입력값이 커지면 커질수록 영향력이 줄어들기 때문이다
O(log n)
로그 복잡도라고 부르며 Big-O 표기법중 O(1) 다음으로 빠른 시간 복잡도를 가진다
이진 탐색 트리와 up&down게임을 예로 들 수 있다

O(n^2)
2차 복잡도(quadratic complexity)라고 부르며, 입력값이 증가하면 n^2의 비율로 시간이 증가한다
for (int i; i < n; i++) {
for (int j; j < n; j++) {
System.out.println("hello");
}
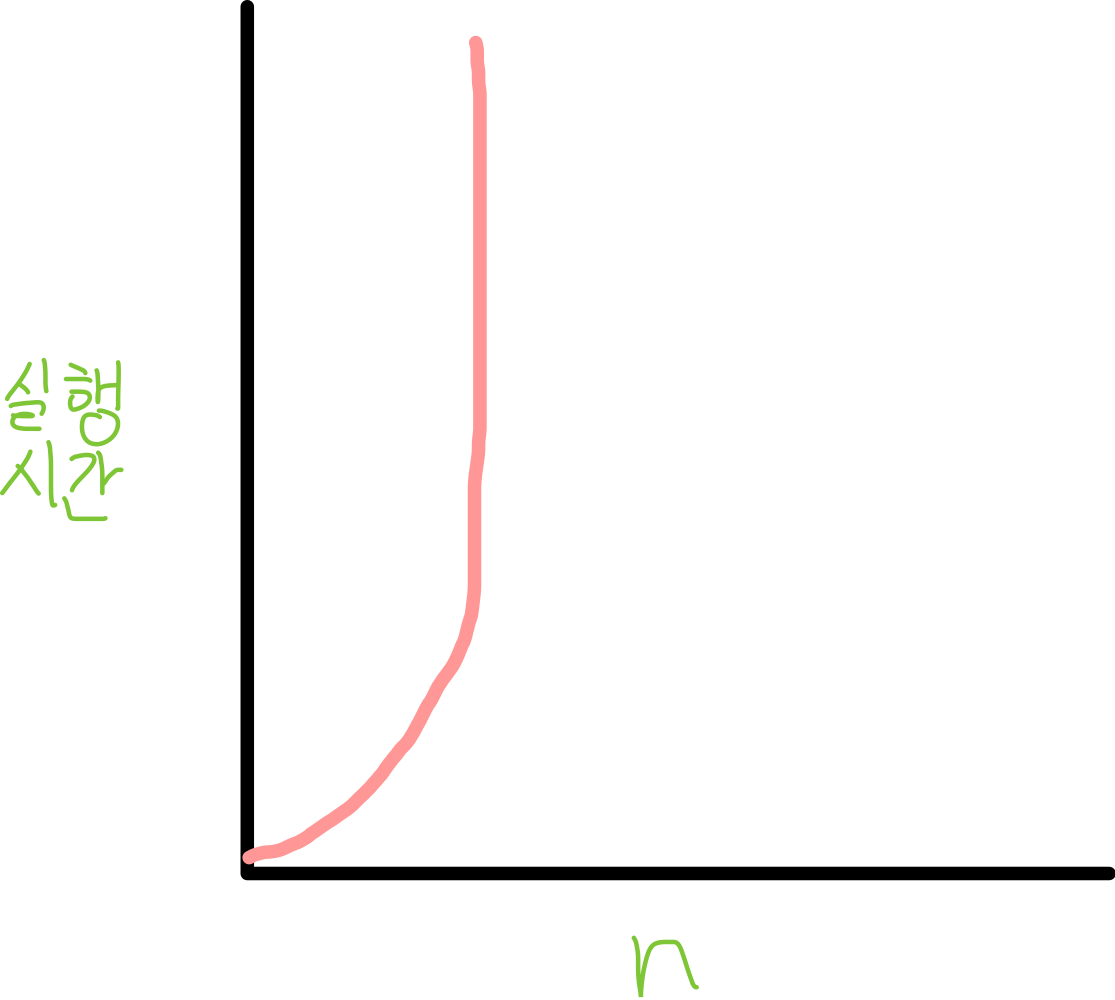
}O(2^n)
기하급수적 복잡도(exponential complexity)라고 부르며, Big-O 중 가장 느린 시간 복잡도이다
구현한 알고리즘이 이 시간 복잡도를 가진다면 다른 방법을 추천한다
// 재귀만로 구현한 피보나치 수열은 기하급수적 복잡도의 대표적인 알고리즘이다
public int fibonacci(int n) {
if(n <= 1) {
return 1;
}
return fibonacci(n - 1) + fibonacci (n - 2);
}
'개발일지 > 컴퓨터지식' 카테고리의 다른 글
| 완전 탐색 알고리즘 (Brute-Force Algorithm) (0) | 2022.10.01 |
|---|---|
| 탐욕 알고리즘(Greedy Algorithm) (0) | 2022.09.29 |
| 자료구조 Deque (0) | 2022.09.28 |
| 자료구조 그래프 Graph (0) | 2022.09.25 |
| 자료구조 트리 Tree (2) | 2022.09.25 |

시간 복잡도
필요로 하는 시간을 따지는 것 : 입력값의 변화에 따라 연산을 실행할 때, 연산 횟수에 비해 시간이 얼마나 걸리는가?
BIig-O 표기법
시간 복잡도를 표기하는 방법은 3가지가 있다
- Big-O (빅-오) - 최악 : "최대 이 정도까지 시간이 걸린다"
- Big-Ω (빅-오메가) - 최선 : "최소한 특정 시간 이상이 걸린다"
- Big-θ (빅-세타) - 평균 : "보통 이 정도 시간이 걸린다"
이 중 Big-O 표기법이 가장 자주 사용된다
다른 방법처럼 최악의 경우가 일어나지 않기를 바라는 것보다는 최악의 경우도 고려하여 대비하는 것이 바람직하다
O(1)
입력값의 크기와 관계없이 같은 시간이 걸린다
constant complexity라고 하며, 입력값이 증가하더라도 시간이 늘어나지 않는다
public static int O_1(int[] arr, int index) {
return arr[index];
}
int[] arr = new int[]{1, 2, 3, 4, 5};
int index = 1;
int results = O_1(arr, index);
System.out.println(results); // 2O(n)
선형 복잡도(linear complexity)라고 부르며, 입력값이 증가함에 따라 시간 또한 같은 비율로 증가한다

public void O_n(int n) {
for (int i = 0; i < n; i++) {
System.out.println("안녕");
}
}
public void O_n2(int n) {
for (int i = 0; i < n * 2; i++) {
System.out.println("안녕2");
}
}❗️ O_n2 알고리즘은 입력값이 1 증가할 때마다 실행시간이 2씩 증가한다
이걸 보고 "그렇다면 이 알고리즘은 O(2n)이라고 표현하는 건가?" 라고 생각할 수 있는데
Big-O 표기법에서는 n앞의 수와 관계없이 모두 O(n)으로 표기한다
입력값이 커지면 커질수록 영향력이 줄어들기 때문이다
O(log n)
로그 복잡도라고 부르며 Big-O 표기법중 O(1) 다음으로 빠른 시간 복잡도를 가진다
이진 탐색 트리와 up&down게임을 예로 들 수 있다

O(n^2)
2차 복잡도(quadratic complexity)라고 부르며, 입력값이 증가하면 n^2의 비율로 시간이 증가한다
for (int i; i < n; i++) {
for (int j; j < n; j++) {
System.out.println("hello");
}
}O(2^n)
기하급수적 복잡도(exponential complexity)라고 부르며, Big-O 중 가장 느린 시간 복잡도이다
구현한 알고리즘이 이 시간 복잡도를 가진다면 다른 방법을 추천한다

// 재귀만로 구현한 피보나치 수열은 기하급수적 복잡도의 대표적인 알고리즘이다
public int fibonacci(int n) {
if(n <= 1) {
return 1;
}
return fibonacci(n - 1) + fibonacci (n - 2);
}
'개발일지 > 컴퓨터지식' 카테고리의 다른 글
| 완전 탐색 알고리즘 (Brute-Force Algorithm) (0) | 2022.10.01 |
|---|---|
| 탐욕 알고리즘(Greedy Algorithm) (0) | 2022.09.29 |
| 자료구조 Deque (0) | 2022.09.28 |
| 자료구조 그래프 Graph (0) | 2022.09.25 |
| 자료구조 트리 Tree (2) | 2022.09.25 |
